染色与染色方法 - (EPUB全文下载)

文件大小：2.57 mb。
文件格式：epub 格式。
书籍内容：

目　录
第一章　染色问题与染色方法
第二章　染色分类，探究解法
2.1　染色与赋值
2.2　染色与覆盖
2.3　表格中的红点问题
2.4　棋盘染色问题
2.5　图论中的染色问题
2.6　几何中的染色问题
2.7　染色极值问题
第三章　竞赛试题选讲
参考答案
高中数学竞赛专题讲座
染色与染色方法
主　编　王慧兴
图书在版编目（CIP）数据
高中数学竞赛专题讲座．染色与染色方法／王慧兴主编．—杭州：浙江大学出版社，2008.8
ISBN 978-7-308-06100-1
Ⅰ．高…　Ⅱ．王…　Ⅲ．数学课—高中—教学参考资料　Ⅳ．G634.603
中国版本图书馆CIP数据核字（2008）第097183号
高中数学竞赛专题讲座（染色与染色方法）
主　　编　王慧兴
责任编辑　徐素君
封面设计　刘依群
出版发行　浙江大学出版社
　　　　　（杭州天目山路148号　邮政编码310028）
　　　　　（E-mail：zupress@mail.hz.zj.cn）
　　　　　（网址：http://www.zjupress.com）
排　　版　杭州大漠照排印刷有限公司
印　　刷　富阳市育才印刷有限公司
开　　本　787mm×960mm　1/16
印　　张　7.25
字　　数　160千
版印次　　2008年8月第1版　2008年8月第1次印刷
书　　号　ISBN 978-7-308-06100-1
定　　价　11.00元
版权所有　翻印必究　印装差错　负责调换
浙江大学出版社发行部邮购电话（0571）88072522
丛书编委会
丛书主编
　　　　陶平生　冯跃峰　边红平
编委名单
　　　　陶平生（江西科技师范学院）
　　　　冯跃峰（深圳中学）
　　　　边红平（武汉钢铁厂第三中学）
　　　　王慧兴（河南实验中学）
　　　　李世杰（衢州市教研室）
　　　　许康华（富阳二中）
　　　　蔡小雄（杭州二中）
编写说明
《高中数学竞赛专题讲座》（第一辑）12种出版以来，反响强烈，深受广大读者喜爱，并收到了大量反馈信息。很多读者，包括一线竞赛辅导的教师和竞赛研究人员提出了许多宝贵的建设性意见，希望我们再组织出版一套以解题方法和解题策略为主的丛书。为了满足广大读者的需求，我们在全国范围内组织优秀的数学奥林匹克教练编写了《高中数学竞赛专题讲座》（第二辑）共8种：《图论方法》、《周期函数与周期数列》、《代数变形》、《极值问题》、《染色与染色方法》、《递推与递推方法》、《组合构造》；考虑到配套，把第一辑中《数学结构思想及解题方法》放在第二辑出版。
丛书的起点是高中阶段学生必须掌握的数学基本知识和全国数学竞赛大纲要求的一些基本的数学思想、方法，凡是对数学爱好的高中学生都有能力阅读。丛书的特点是：
1．充分吸收了世界各地的优秀数学竞赛试题，通过对典型例题的解剖，传授数学思想方法，侧重培养学生的逻辑思维能力，不唯解题而解题；
2．本着少而精的原则选择材料，不搞题海战术，不追求大而全，而是以点带面，举一反三；
3．以数学修养和能力培养为立意，通过深刻剖析问题的数学背景，挖掘数学内涵，培养学生的数学品格和解决实际问题的能力；
4．在注重基础知识训练同时，有适当程度的拨高，对参加冬令营甚至是更高层次的竞赛都有相当的指导作用和参考价值。
丛书由陶平生、冯跃峰、边红平主编；参加编写的成员是：陶平生、冯跃峰、边红平、王慧兴、李世杰、蔡小雄、许康华。
鉴于我们的水平有限，书中的不妥之处敬请读者批评指正。
第一章　染色问题与染色方法
染色问题和染色方法是两个不同的术语，前者是说题目给出了一种染色方法，在给定的染色条件下，提出一个待解决的问题；后者通常是题目没有提到染色，解题者为了解决问题，自觉探究一种染色方法，使问题得到解决．与染色相关的问题通常表现出某种不确定性，多归属于组合问题．染色问题多而杂，但主要分为两类：对边染色和对点染色．解决染色问题的基本方法有逐步调整法、整体处理法、不变量法、赋值计算法、极端性方法以及递推方法等等；染色问题中的存在性问题通常可考虑抽屉原理．
例1　设O是线段AB的中点，点A1
，A2
，…，An
在线段OA上，点B1
，B2
，…，Bn
在线段OB上，并且点Ai
与Bi
（i＝1，2，…，n）关于点O对称，将其中n个点染红色，另n个点染蓝色．求证：所有红点到点A的距离之和等于所有蓝点到点B的距离之和．（1985年北京市数学竞赛题）
解　对一种具体染色S，记所有红点到点A的距离之和为Sh
，所有蓝点到点B的距离之和为Sb
．
第一步，考察极端情况：如果线段OA上的点A1
，A2
，…，An
都是红点，则线段OB上的点B1
，B2
，…，Bn
都是蓝点，由对称性，得OAi
＝OBi
（i＝1，2，…，n），从而
第二步，对任一染色方法，证明Sh
＝Sb
，为此我们应用逐步调整法来证明Sh
－Sb
是不变量．
如果一种染色S，在线段OA上存在一个蓝点P，则在线段OB上必存在一个红点Q，我们改变一下这两个点的颜色，即P（蓝→红），Q（红→蓝），这样，我们得到另一种染色方法S′，计算，
S′h
＝Sh
－AQ＋AP＝Sh
－PQ，
S′b
＝Sb
－BP＋QB＝Sb
－PQ，
∴　Sh
－S′h
＝Sb
－S′b
，即Sh
－Sb
＝S′h
－S′b
．
故　Sh
－Sb
是不变量．
∵　经过有限次上述操作，我们可以把染色S变换成上述极端情况．
∴　由上述不变量，得Sh
－Sb
＝0，即Sh
＝Sb
．
例2　平面上任给n个互异的点，每两点连一条线段，再将所得的
条线段的中点染红色，求红点个数的最小值．（1991年亚太地区数学竞赛题）
解　我们利用极端性原理实现隔离计数．
第一步，设n个点共线，顺次记为A1
，A2
，…，An
，且记线段A1
An
的中点为P，则n ............

书籍插图：

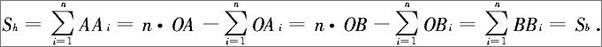
以上为书籍内容预览，如需阅读全文内容请下载EPUB源文件，祝您阅读愉快。