计算进化史：改变数学的命运 - (EPUB全文下载)

文件大小：0.7 mb。
文件格式：epub 格式。
书籍内容：

译者序
介绍数学史的书有很多，这一本却不太一样。
说起数学史，也许你会想到课本里各种定理前耳熟能详的名字，他们是代表人类最高智慧的璀璨群星。数学家们提出的定理，以及这些定理的证明，构成了数学史上一个又一个里程碑。然而，在浩如烟海的数学史中，本书作者却独辟蹊径，挑出了一条似乎并不那么耀眼的主线——计算。
古代的人们已经开发出各种方法来丈量土地、计算税收。无论是本书中提到的美索不达米亚，还是我们中国人熟知的《九章算术》等书，都体现了古人在计算方面的杰出成就。然而随着问题范畴不断扩大，“无穷”超出了计算力所能及的范围，于是古希腊人以“推理”奠定了公理化方法的根基。
从希尔伯特提出的用计算来代替推理的宏伟猜想，到可计算性理论与构造理论，再到通过计算机进行海量计算来完成证明，“推理”和“计算”在20世纪经历了反复的争斗。和科学史上的许多争论一样，重要的不是争论本身的结果，而是这一过程带来了学科的巨大发展，甚至创立出很多新的学科分支。我们在书中既可以看到眼下函数式编程里最常见的λ表达式的历史渊源，也能看到四色定理的计算机证明等我们熟知的数学里程碑。到底能不能用计算规则取代公理或许还悬而未决，但在数学家的工作中，计算的角色越来越显著这一趋势似乎已无可逆转，计算正在以一种全新的方式引领数学的前进。
“计算”这条主线看似简单，却牵涉到了哲学、逻辑、语言学、计算机科学等诸多领域。对于这些有些抽象乃至艰涩的内容，作者用通俗易懂的语言，清晰地把握概念而不过多地涉及学术细节，在必要处又用简明的算法示例与生动的故事加以介绍，充分展现了“大家写小书”的风范。在如今这个时代，计算机科学，特别是算法逐渐占据了我们的工作和生活每一个角落，对“计算”本身多一些了解和思考，应该说是十分有益甚至必要的。也许这本书中提到的某个领域，能够激起读者的兴趣，引发进一步的探索和研究呢。
感谢戴童编辑的大力支持，令译稿增色不少。感谢多维克教授解答翻译过程中遇到的疑问。
感谢我的父母和妻子在背后的支持与付出。
受译者水平所限，文字中的疏漏和不当之处在所难免，还请读者批评指正。
劳　佳2016年10月于加州
致热拉尔·于埃
感谢对本书做出贡献的学者及编校人员，他们是：
帕布罗·埃里奇、苏菲·班凯尔、雅克·德尚、乔艾尔·傅埃、苏菲·卡勒耐克、朱塞佩·隆戈、亚历山大·米凯尔、蒂埃里·包利、本杰明·维尔纳
前言　数学踏上新的征程
人们常说，刚刚过去的一个世纪是数学真正的黄金时代。数学在20世纪的进步比先前所有的世纪加起来还要大。然而，刚刚开始的这个世纪也可能同样是数学发展的好时候。或许，数学在这个世纪的变迁会和20世纪一样巨大，甚至更为惊人。引发这种想法的信号之一是一场渐变：自20世纪70年代开始，数学方法的基石——证明的概念逐渐发生演变，让一个古老却有些被人忽视的数学概念重新回到了舞台中央，这就是“计算”。
计算能成为引发革命的导火索，这看起来有点不合常理。算法，比如做加法和做乘法的算法，常常被视为数学知识中最基础的一部分，做计算也经常被看成是缺乏创造性的枯燥工作。数学家们自己对计算也颇有成见，勒内·托姆就曾说过：“我的论述中很大一部分属于纯粹的猜想，大家基本上可以把它们看成是梦话。我接受这种定性……如今，世界上到处有这么多学者在做计算，难道有人做梦不是件好事吗？”用计算来做梦，大概还真有点难度啊……
不幸的是，对计算的偏见恰恰根植于“数学证明”这一概念的定义里。确实，欧几里得以降，“证明”的定义就是利用公理和演绎规则构建的一套推理。然而，要解决一个数学问题，仅仅需要构建一套推理吗？数学的实践难道没有告诉我们，解决问题需要把推理的步骤和计算的步骤巧妙地融合起来吗？公理化方法若局限在推理中，它所展现的数学视野恐怕也会十分狭隘。正是因为人们对约束过多的公理化方法多有批评，才让计算有机会重新出现在数学的舞台上。现在，已有一些研究工作（它们之间未必有关联）渐渐开始质疑推理高于计算的优势地位，并倡导一种更为平衡的观点，让两者互为补充。
这场革命让我们重新考量推理和计算之间的关系，同时也促使我们重新审视数学与物理学、生物学等自然科学之间的对话，特别是数学为何能在这些学科中发挥难以理解的强大作用这一古老问题，以及自然理论的逻辑形式这一全新问题。此外，这场革命给“分析判断”和“综合判断”等哲学概念带来了新的火花。它还让我们反思数学与计算机科学之间的关系，而且数学似乎是唯一一门不需要借助机器的科学，它为什么如此独特？
最后，最振奋人心的是，这场革命让我们隐约看到了一些解决数学问题的新方式，它摆脱了过去的技术强加给证明长度的枷锁——数学也许正踏上新的征程，去探索从未涉足的全新领域。
诚然，公理化方法的危机并不是凭空出现的。从20世纪上半叶起就有许多先兆，特别是两种理论——可计算性理论和构造性理论的出现。这两种理论本身虽然没有质疑公理化方法，却重新确立了计算在数学大厦中的地位。在讨论公理化危机之前，我们会简要回顾这两个概念的历史。不过，还是让我们先上溯远古，探寻计算这一概念的起源，看看古希腊人对数学的“发明”过程吧。
第一篇　古老的起源
第1章　从史前数学到希腊数学
数学史往往是从公元前5世纪的希腊开始讲起的。毕达哥拉斯创立了算术，泰勒斯和阿那克西曼德创立了几何，奠定了古代数学的两大分支。算术和几何的创立，无疑是数学史上的重大突破。然而，这样的讲法却忽略了一个重要的时代，也就是所谓的“史前”数学。人们并没有等到公元前5世纪才开始解决数学问题，特别是那些日常面临的具体数学问题。
会计师和土地测量师
“数学”活动最古老的痕迹之一是在美索不达米亚发现的一块泥板，它可以追溯到公元前2500年。这块泥板记录了这样一个计算：如果一个谷仓里有1152000份粮食，每个人分得7份，一共可以分给多少人呢？不出所料，结果是164571人，即用1152000除以7得到的结果。看来，美索不达米亚的会计师在算术“诞生”之前很久就知道怎么做除法了。甚至，书写完全有可能就是为了记账才发明的——虽然这些事情很难说得准，但 ............

书籍插图：

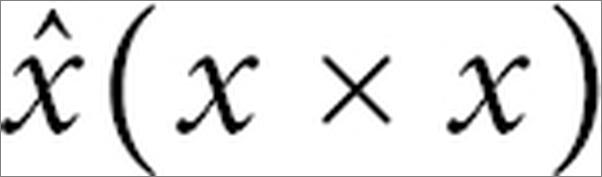
以上为书籍内容预览，如需阅读全文内容请下载EPUB源文件，祝您阅读愉快。