如何培养逻辑脑：聪明人都在玩的逻辑游戏 - (EPUB全文下载)

文件大小：5.65 mb。
文件格式：epub 格式。
书籍内容：

如何培养逻辑脑：聪明人都在玩的逻辑游戏
（英）菲利普斯　著
九州出版社
图书在版编目（CIP）数据
如何培养逻辑脑：聪明人都在玩的逻辑游戏/（英）菲利普斯著；李俊译.——北京：九州出版社，2015.11
ISBN 978-7-5108-4015-9
Ⅰ.①如…　Ⅱ.①菲……②李…　Ⅲ.①智力游戏　Ⅳ.①G898.2
中国版本图书馆CIP数据核字（2015）第256603号
如何培养逻辑脑：聪明人都在玩的逻辑游戏
作　　者：（英）查尔斯·菲利普斯
翻　　译：李　俊
出 版 人：黄宪华
地　　址：北京市西城区阜外大街甲35 号(100037)
发行电话：(010)68992190/3/5/6
网　　址：www.jiuzhoupress.com
电子信箱：jiuzhou@jiuzhoupress.com
印　　刷：三河市华成印务有限公司
开　　本：787 毫米×1092 毫米 32 开
印　　张：5.5
字　　数：40 千字
版　　次：2015 年12 月第1 版
印　　次：2015 年12 月第1 次印刷
书　　号：ISBN 978-7-5108-4015-9
定　　价：32.00 元
版权所有 侵权必究
目录
扉页
版权信息
引言
测试一
题目 01 5个球
题目 02 雪花数字
题目 03 蜂窝灵感Ⅰ
题目 04 数字金字塔
题目 05 航海寻宝Ⅰ
题目 06 旋转的六边形Ⅰ
题目 07 数字路径
题目 08 酒“迷”人
题目 09 地砖拼图
题目 10 7的倍数
题目 11 酒吧颜色运算Ⅰ
题目 12 名片游戏Ⅰ
题目 13 数字“分子”Ⅰ
题目 14 园艺路径
题目 15 特殊的数独游戏
题目 16 月球和卫星
题目 17 赌徒的梦I
题目 18 252
题目 19 符合逻辑的书架
题目 20 骰子间的运算
题目 21 如何停车入库
题目 22 时钟解码I
题目 23 酒窖藏酒
题目 24 标准4杆I
题目 25 祝福卡片上的逻辑题
测试一 答案
测试二
题目 26 6的倍数
题目 27 猜猜“？”是几
题目 28 名片游戏Ⅱ
题目 29 几何图形蛋糕
题目 30 1989年3月6日
题目 31 牌弈
题目 32 国际跳棋
题目 33 蜂窝灵感Ⅱ
题目 34 航海寻宝Ⅱ
题目 35 扭曲的蜂窝数字题
题目 36 图层模块
题目 37 “五月皇后”的花冠
题目 38 数字“分子”Ⅱ
题目 39 名片游戏Ⅲ
题目 40 标准4杆Ⅱ
题目 41 试卷中的路径题
题目 42 酒吧颜色运算Ⅱ
题目 43 时钟解码Ⅱ
题目 44 冰块挑战
题目 45 瓷砖逻辑
题目 46 连梯游戏
题目 47 旋转的六边形Ⅱ
题目 48 赌徒的梦Ⅱ
题目 49 航海寻宝Ⅲ
题目 50 旋转的陶盘
测试二 答案
思维能力评分表
“人在智慧上、精神上的发达程度越高，人就越自由，人生就越能获得莫大的满足。”
引言
在生活中，数字、图形元素以及其他有趣的符号组合，总是能优雅地呈现出某些规律，而人类似乎天生就会注意和欣赏这些规律。
为了生存，人类在几千万年的进化过程中，自然而然地对周围的环境产生好奇心和警惕心。我们的祖先在恶劣的自然环境下必须提防天敌，因而逐渐发现能够保护自己的生物规律和颜色特点等，也就是说，为了保证生存，人类需要安全合理地利用它们。关于我们身边的各种数字、图像规律，我会在“聪明人都在玩的脑力游戏”系列中一一介绍。了解事物如何彼此关联、运作是人类的本能，这对于我们在科学和思想方面取得突破性进展也有很大帮助。
在日常生活中，有两个大家非常熟悉的规律：月亮的盈亏和四季的变化。与祖先相比，现代人对月亮的盈亏注意得相对较少，但是月亮的变化仍然影响着我们的生活。有时，我们可能会受到好奇心的驱使，在一些随机的数字中发现规律，比如朋友、亲人的生日，或是每天乘坐的公交车编号。我们在自然界中也会发现各种规律，比如，你在沙滩散步时捡到一个贝壳，可能会观察到上面有规则的螺旋图案，又或者你在公园中看到一棵树，发现这棵树的树叶有一定的生长规律。
让我们来认识一个有趣的数字序列——斐波那契数列：从0和1开始，后面的数字是它前面两个数字的和，比如0、1、1、2、3、5、8、13、21、34、55……这个序列非常有名，以意大利的列昂纳多·斐波那契（Leonardo Fibonacci，1170-1250年）的姓命名，而斐波那契本人也以描述这个序列的《算盘书》（1202年）闻名于世。
树叶螺旋式生长在树干上，因为这样树叶之间就不会相互重叠，每片树叶都可以被阳光照射到，而斐波那契数列明确地用数字表示了这种螺旋式规律。除了贝壳和树叶，我们还可以在松果或向日葵花盘等许多事物中发现这种规律。
繁衍的兔子
斐波纳契在《算盘书》中介绍，他在观察兔子繁衍的过程中进行了关于斐波那契数列的思考，具体如下：将一对新出生的兔子（一只公兔和一只母兔）放生到田野，它们大概在一个月左右开始第一次交配，再过一个月的时间就可以生出新兔子。假设，一只母兔一次会生出一只公兔和一只母兔，并且所有的兔子都能够存活下来，那么，一年后这片田野总计会有多少对兔子？
参考斐波那契数列得出答案：第一个月，一对（最初的那一对兔子）；第二个月，一对（还没有新的兔子出生）；第三个月，两对（最初的那一对和它们新生出的小兔）；第四个月，3对（最初的那一对又生了一对，而先出生的那一对还没有生出小兔），以此类推。根据题目的假设，12个月之后一共有233对兔子。如果你从0开始算起，那就要参考斐波那契数列中的第13个数字（之所以要用第13个数字，是因为第12个数字是第12个月开始时兔子的数量，而不是第12个月结束以后兔子的数量）。
数字序列的韵律
人们通常认为上述序列是斐波那契发现的，所以用他的姓来命名。但是事实上，这个特殊而又充满魅力的数字序列可以追溯到很久以前，它在公元前450年的印度第一次被发现。数学作家马库斯·杜·索托伊（Marcus du Sautoy）认为，印度数学家首先发现了数字序列中的某些数字可以组成长长短短 ............

书籍插图：

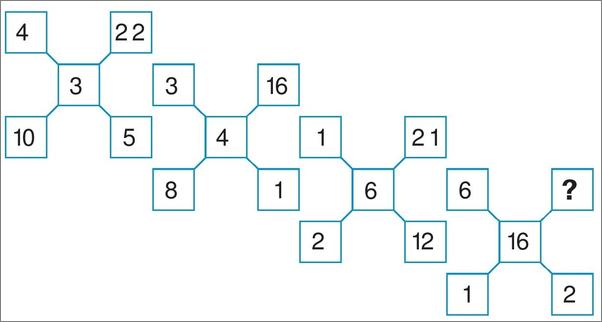
以上为书籍内容预览，如需阅读全文内容请下载EPUB源文件，祝您阅读愉快。