超越无穷大：一次跨越数学边界的冒险之旅 - (EPUB全文下载)

文件大小：2.8 mb。
文件格式：epub 格式。
书籍内容：

超越无穷大：一次跨越数学边界的冒险之旅
[英]尤金妮娅·程 著
杜娟 译
中信出版集团
目录
题记
序言
第一部分 旅程
1 数学世界里的尼斯湖水怪
2 希尔伯特旅馆实验
3 无穷不是自然数
4 有理数和无理数
5 一个函数问题
6 接近无穷
7 超越无穷
8 无穷vs无穷
9 无穷是什么？
第二部分景色
10 抽象事物
11 从千层酥到iPod
12 维度问题
13 范畴论和结合体
14 无穷小
15 分裂
16 古怪的终极难题
17 跨越逻辑边界
致谢
版权页
题记
纪念萨拉·巴德尔（Sara Al-Bader）
她教会我有限的生命里可以容纳无穷的爱
序言
我讨厌机场。
我觉得机场让人特别有压力，拥挤而且吵闹。机场里总是充斥着过多的人、过多的队列、过少的作为和无处不在诱惑着我的不健康的食物。非常不幸的是，旅程总是从机场开始，这让我有一点儿害怕旅行。旅行应该是一个令人兴奋的有关发现的过程，坐着飞机去一个新的地方，应该是一段壮美而充满魔力的经历。但是机场和狭窄的经济舱座椅经常会毁掉这一切。
学习数学应该也算得上一段令人兴奋的发现之旅，同样壮美且充满魔力，尽管它的开端也经常会毁掉一切。因为一开始你总是会遇见大量的事实、公式、让人感到压力的测试和等待解决的乏味问题。
相较坐飞机，我喜欢乘船旅行。
我喜欢身处开阔的水面，感受风吹过我的脸庞，看着远处的楼群和海岸线，但是又不用靠近。我喜欢一直朝着地平线前进，但是又永远不会到达。我喜欢感受自然的力量，但是又不用完全受大自然的摆布。我不是一个水手，所以通常掌控船的另有其人。偶尔我会遇到一些能够操作的船，这样一来，能够发挥我自己的能力就成了一种奖励。我曾经划着一艘小的手划艇沿着包围着一座小小的法国城堡的护城河漫游，我也曾经沿着阿姆斯特丹的运河踩脚踏船，我还曾经沿着康河撑篙。不过，在一次失足落水之后，我就再也不到康河撑篙了，这和有些人最初在数学领域经历了一些挫折之后就再也不碰数学是一样的。我曾经在悉尼和洛杉矶乘船去看生活在离海岸很远的地方的大鲸鱼，也曾经在威尔士乘船去离海岸很远的地方看海豹和其他野生生物。我小的时候总会和家人一起坐着渡轮跨过英吉利海峡到法国度假，直到几乎不可能建成的欧洲之星变成现实。由此可见，我们人类是多么容易把之前看来几乎不可能的事情当作理所应当！
现在，我很少再为了到达某个目的地而乘船了。相反，我的目的就是享受乘船的过程，欣赏沿海风光和大自然，偶尔发挥一下我自己的能动性。一个例外就是泰晤士河上的渡轮，因为乘坐泰晤士河上的渡轮是伦敦市中心一种令人非常享受的通勤方式。它既能让乘客享受到乘船的乐趣，又能帮助乘客到达目的地。
在某种程度上，我喜欢抽象数学这件事和我喜欢乘船有点儿类似。对于我来说，这两者都超越了到达一个目的地的范畴，更多的是乐趣、锻炼头脑、与数学交流和欣赏数学之美。这本书是一个通往神秘而壮美的“无穷”世界的旅程。我们即将看到的风景会让我们大开眼界，惊叹不已，甚至有的时候会让我们觉得不可思议。我们将会沉浸在数学的魔力里，但是又不用完全受其摆布。我们将会朝着人类思想的地平线前进，但是又永远不会到达。
第一部分　旅程
1　数学世界里的尼斯湖水怪
无穷就像尼斯湖水怪，以其令人惊叹的体型和难以捉摸的个性，吸引人们展开想象。无穷是一场梦，一个巨大的由无穷无尽的时间和空间所构成的迷幻世界。无穷是一个黑暗森林，在里面，你会遇见超越想象的生物、纠缠在一起的灌木丛和突然照射进来的阳光。无穷是一个环形，它在我们面前呈现为一个无穷无尽的螺旋。
我们的生活是有限的，我们的头脑是有限的，我们所处其中的世界也是有限的。但是我们仍旧能够瞥见我们周围的无穷。我小时候生活的房子中间有一个火炉，火炉上有一个烟囱。所有的房间都围绕着这个火炉连接在一起。这意味着我和妹妹可以一圈一圈地相互追逐，没有终点，感觉上就好像我们生活在一个无穷大的房子里一样。环形让人们可以在有限的空间里开启一个无穷的旅程。这个原理不仅仅被用在了孩子们的相互追逐上，还被用在了汽车赛道上和粒子对撞机上。
后来，我的母亲教我使用频谱计算机编程。直到现在，每当想起我最喜欢的计算机小程序时，我都还是会不由自主地笑出来。
10 打印输出“你好”
20 返回到10
这些计算机语句能够产生一个无穷无尽的循环。当然，这是一个抽象概念的循环，而不是一个物理上的循环。每到这种时候，我就会点击“开始”，然后非常兴奋地看着“你好”这个词在屏幕上滚动。因为我知道，除非我点击“结束”，否则这个过程就会永远重复下去。我是那种不会轻易感到厌烦的孩子。我每天都会这么做，而不觉得自己应该赶紧写一些更加有用的程序。不幸的是，这也使得我的编程能力从来没有真正进步过。无穷的耐心导致了一个奇怪的后果。
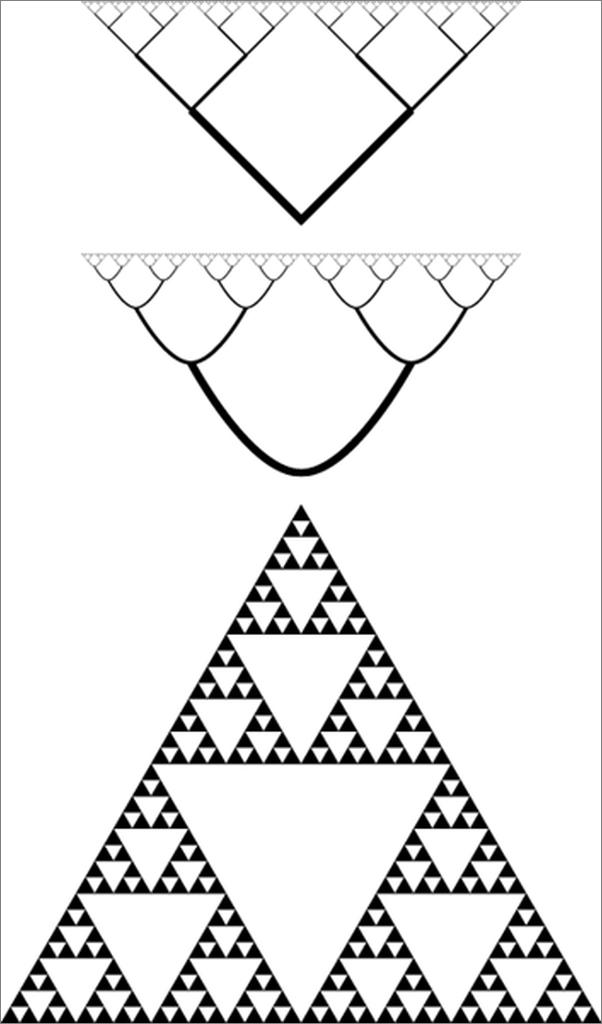
我的这个简短但能产生冗长的打印输出结果的抽象循环背后的原理是：程序会自己回到原点。自我索引让我们能够从另一个角度窥测无穷。分形是用和自身形状相同的形状构建的形状。当你把其中的一部分放大的时候，你看到的将是相同的形状。为了达到这一目的，这个形状的细节需要能够“永远”保持下去。毋庸置疑，这些细节一定会超越我们能够描绘和能够看到的极限。图1–1描绘了一些分形树和著名的谢尔宾斯基三角（Sierpinski triangle）的最初几级。
图1–1
如果你把两面镜子对在一起，你看见的将不再仅仅是自己的镜像，还有你的镜像的镜像。你的镜像的镜像又会产生出自己的镜像。只要你调整镜子的角度，这些镜像就会一直叠加下去。每一个镜像都会比前面的镜像小，从理论上讲，它们会像分形一样“无穷”延续下去。
我们能够从环形和自我索引中看到无穷，同样也能从镜子里的镜像越来越小这件事情上看到无穷。孩子们为了能够让自己一直吃到蛋糕，每次都只吃剩余的蛋糕的一半。一群人在分享一个蛋糕的时候，都很谦让，不愿意吃最后的一块，所以每个人都吃剩余部分的一半。有人告诉我日语里有一个专门形容这个现象的词——“enryo no katamari”，意思就是大家都很谦让而不愿意吃的最后一点蛋糕。
我们并不确切地知道宇宙是不 ............

书籍插图：

以上为书籍内容预览，如需阅读全文内容请下载EPUB源文件，祝您阅读愉快。